[알고리즘 트레이딩] KPSS 검정: 시계열 정상성 분석
1. KPSS 검정이란?
KPSS(Kwiatkowski-Phillips-Schmidt-Shin) 검정은 시계열 데이터가 정상적인지(stationary) 아닌지를 평가하는 통계적 방법입니다. 시계열 분석에서 정상성 여부는 데이터의 예측 가능성과 분석 가능성을 결정하는 중요한 요소입니다.
KPSS 검정은 귀무가설(null hypothesis)이 정상성을 가정하는 특징을 갖고 있습니다. 즉, p-value가 낮으면 정상성이 기각되며 데이터가 비정상적(Non-Stationary)임을 의미합니다.
2. KPSS 검정의 원리
KPSS 검정은 시계열 데이터를 다음과 같이 분해하여 분석합니다:
-
-
-
여기서 랜덤 워크(R_t)의 존재 여부를 검증하는 것이 KPSS 검정의 핵심입니다. 만약
3. KPSS 검정 알고리즘
3.1. 잔차(Residual) 계산
시계열 데이터에서 추세 성분을 회귀 분석(OLS: Ordinary Least Squares)으로 제거하고, 잔차를 계산합니다:
-
여기서
-
이후 잔차를 누적하여 새로운 시계열
3.2. 누적 잔차(Sum of Residuals) 계산
잔차를 누적하여
3.3. KPSS 통계량 계산
KPSS 검정의 핵심 공식은 다음과 같습니다:
-
-
-
이 통계량이 비정상적인 경우 커지게 되며, 특정 임계값과 비교하여 정상성 여부를 판별합니다.
4. KPSS 검정 결과 해석
-
p-value > 0.05 → 귀무가설(Stationarity) 채택 → 정상성 있음 ✅
-
p-value < 0.05 → 귀무가설 기각 → 비정상적인 시계열 데이터 ❌
5. Python을 이용한 KPSS 검정 구현
Python의 statsmodels 라이브러리를 사용하여 KPSS 검정을 수행할 수 있습니다.
import numpy as np
import statsmodels.api as sm
from statsmodels.tsa.stattools import kpss
# 예제 시계열 데이터 생성 (랜덤 워크)
n = 100
np.random.seed(42)
X = np.cumsum(np.random.normal(size=n)) # 누적합(랜덤 워크)
# KPSS 검정 수행
stat, p_value, _, crit_vals = kpss(X, regression='c', nlags="auto")
# 결과 출력
print(f"KPSS 통계량: {stat}")
print(f"p-value: {p_value}")
print(f"임계값: {crit_vals}")
# 해석
if p_value < 0.05:
print("비정상적인 시계열 데이터 (Non-Stationary)")
else:
print("정상적인 시계열 데이터 (Stationary)")
6. R을 이용한 KPSS 검정 구현
urca 패키지를 활용하여 R에서도 쉽게 KPSS 검정을 실행할 수 있습니다.
library(urca)
# 예제 데이터 생성
set.seed(42)
X <- cumsum(rnorm(100)) # 랜덤 워크
# KPSS 검정 수행
kpss_test <- ur.kpss(X)
summary(kpss_test)
7. 결론
-
KPSS 검정은 시계열의 정상성 여부를 판단하는 중요한 통계 기법이다.
-
정상적인 시계열이면 KPSS p-value가 0.05보다 크다.
-
비정상적인 시계열이면 p-value가 0.05보다 작아진다.
-
Python (
statsmodels.tsa.stattools.kpss)과 R (urca::ur.kpss)를 활용하여 간단히 실행 가능하다.
KPSS 검정은 시계열 분석에서 필수적인 기법이며, 특히 금융 데이터 분석, 예측 모델링, 통계적 투자 전략에서 널리 활용됩니다.




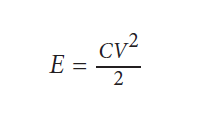

댓글
댓글 쓰기